
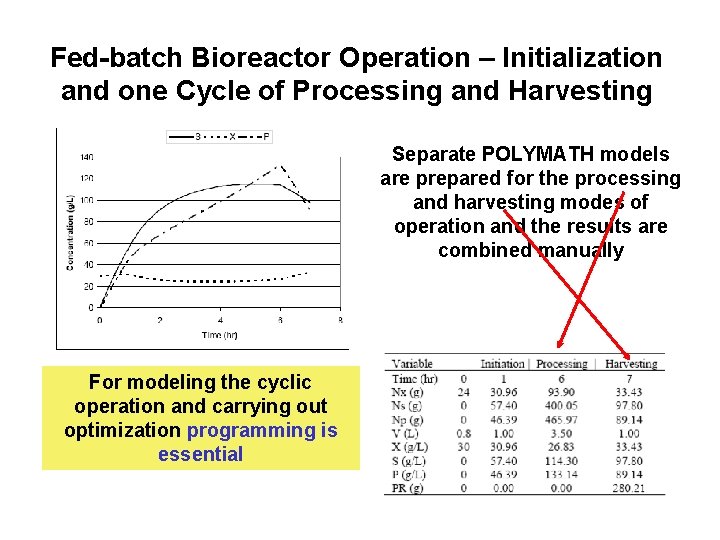
MATLAB Solution for Part B of the Assignment b. MATLAB Main Program – Distillation Period Calculations 2nd layerĭistillation Period Calculations – Converting the Differential Equations to Implicit Algebraic Equations for solving the DEA System MATLAB Main Program – Heating Period Calculations for Various Initial n-octane Mole Fractions Upper layer 2nd layer 1st layer Polymath Generated MATLAB Formatted Model the Distillation Period Semi-Batch Distillation - Change of Temperature and Organic Phase Composition During Distillation

Partial POLYMATH Results for the Distillation Period POLYMATH Program for Simulating the Distillation Period ( 1st layer) Following the bubble point curve with controlled integration Calculate and plot the still temperature (T), component mole fractions inside the still (x1, x2, y1, and y2) and the component mole fractions in the distillate (x1dist and x2dist) using the data and the initial values provided. Partial POLYMATH Results for the Heating Period Bubble point equation f(T) = 0 POLYMATH Program for Simulating the Heating Period (1st layer)
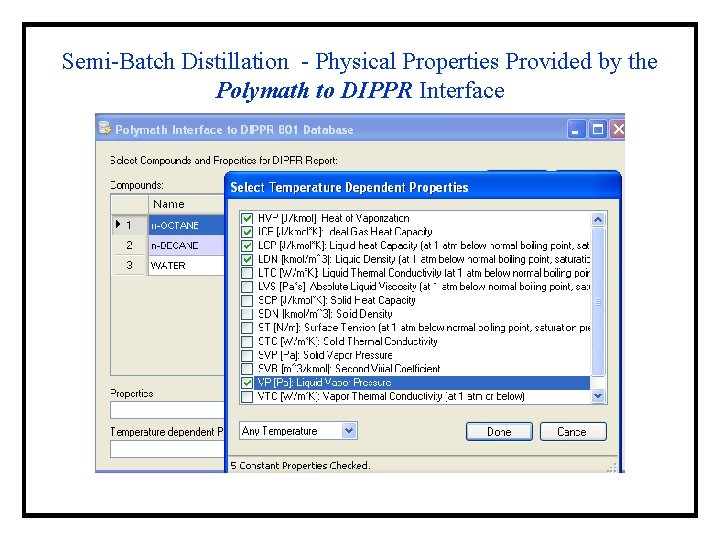
Semi-Batch Distillation - Physical Properties Provided by the Polymath to DIPPR Interface Unique variable name Units and uncertainty in comments Valid temperature range Ideal gas enthalpy equation in a “comment” Semi-Batch Distillation - Physical Properties Provided by the Polymath to DIPPR Interface Semi-Batch Distillation - Physical Property Needs and Sources for the Original Reference* *Prenosil, J. Semi-Batch Distillation - Distillation Period Equations Solving with Polymath the “controlled integration technique” is used for adjusting the temperature to follow the bubble point curve where

Semi-Batch Distillation - Heating Period Equations Mass balance on the water phase yields Stopping Criterion "Semi-Batch Steam Distillation of a Binary Organic Mixture ", Chem. Vary the feed concentration in the range where the requirement for the n-octane concentration in the distillate is attainable. Compute the percent recovery of n-octane in the distillate as function of its concentration in the feed. Determine the lowest n-octane mole fraction in the feed that can yield a distillate concentration of 90% of n-octane. Semi-Batch Distillation - Problem Statement The ambient pressure is P = 9.839E+04 Pa. The ambient temperature is TE = 25 ☌ and the heat transfer coefficient between the still and the surrounding is U = 1.05 J/s-K. All the steam is assumed to condense during the heating period. Starting at time t = 0, steam at a temperature Tsteam = 99.2 ☌ is bubbled continuously through the organic phase at the rate of MS= 3.85e-5 kmol/s. The initial temperature in the still is T0 = 25 ☌. Initially M = 0.015 kmol of organics with composition x1 = 0.725 is charged into the still. The data provided by Ingham et al.are the following. Semi-Batch Distillation - Problem Statement Consider the semi-batch steam distillation of an n-octane (comp. Mordechai Shacham Department of Chemical Engineering Ben-Gurion University of the Negev Beer-Sheva, Israel May 21, 2012 From Punched Cards to Modular and Multilayer Modeling – Forty Years of Computer Based Problem Solving in Chemical Engineering.


 0 kommentar(er)
0 kommentar(er)
